作者:银河期货金融衍生品研究所高级研究员 沈忱
上海财经大学统计与数据科学学院博士生 张偲嘉
本文原载《债券》2025年6月刊
摘 要
2024年9月13日,中金所开启国债期货期权仿真交易,标志着我国场内利率期权品种正式上市,填补了我国期权领域空白。本文比较了常见的期货期权定价模型和波动率的估计方法,选取定价效率较高的BAW模型,利用国债期货历史数据,对国债期货期权进行了理论定价。通过实证分析,本文尝试描述国债期货期权价格的时间价值衰减过程及其与标的价格之间非线性的变化关系,以期投资者在合约正式上市之前,对国债期货期权的价格特征有初步的了解。
关键词
国债期货期权 理论定价 实证分析 价格特征
背景介绍
作为利率市场化的产物,利率衍生品工具在管理利率风险、稳定资本市场、促进经济平稳发展等方面发挥着积极作用。与海外相比,我国国债及其衍生品市场起步较晚,但发展迅速。当前,我国债券市场规模已居全球第二,陆续上市的一系列国债期货产品市场活跃度也不断提升。中金所数据显示,截至2024年,我国国债期货日均成交约22.88万手,日均持仓约49.16万手,分别较上年增长约17.7%和20.5%,保持两位数的增幅。
随着我国债券市场规模的不断扩张以及高水平对外开放稳步推进,市场各方对更加丰富的利率衍生品工具的需求有所上升。从海外实践来看,美国、欧洲、日本等海外发达经济体均已陆续建立了国债期权市场,并与期货市场共同形成了利率风险管理体系的双支柱。目前,中金所也在已上市国债期货合约的基础上,研究设计了2年期、5年期、10年期和30年期国债期权仿真合约,并于2024年9月13日开启仿真交易。
我国国债期货期权上市渐近,本文在中金所合约规则的基础上,利用现有数据和模型为国债期货期权进行理论定价。在精确刻画期权非线性收益结构的同时,理论定价可以帮助投资者提前熟悉和了解不同市场条件下的期权价格波动、时间价值衰减等特征,从而更好地理解期权所蕴含的风险。此外,未来期权合约上市后,投资者也可以根据理论价格来协助判断市场价格是否合理,从而发现潜在的套利机会,并测试开发不同的期权交易策略。
模型介绍
(一)期权的定义
期权是一种金融衍生工具,赋予买方在约定期限内按约定价格买入或卖出一定数量的某种资产的权利,且买方没有必须行权的义务。非线性的收益结构使得投资者在利用期权对冲市场风险或构建投资组合时具有独特的优势,包括相对可控的风险、策略的多样性等。
期权分类标准较多,最简单的分类方式是按买方权利将其分为看涨期权和看跌期权。看涨期权的买方有权按事先约定的行权价格买入标的资产,看跌期权的买方则可以按行权价格卖出标的资产。而按行使权利的时间又可以将期权分为欧式期权和美式期权。欧式期权的行权时间固定,买方只能在到期日行权;美式期权的买方则可以在到期日之前的任何时间行权。美式期权行权方式上较高的灵活度也使得其在定价方面与欧式期权存在一些差异。
(二)常见期权定价模型
期权的理论价格取决于多个因素,包括标的资产价格、行权价格、到期时间、波动率等。而在期权定价研究领域,定价方法主要分为解析类和数值类。解析类通常以传统的Black-Scholes(BS)模型为基础,对于欧式期权,通过构造一个由期权和标的所组成的无风险交易组合,在无套利的条件下推导出微分方程的解析解,为期权进行定价。而数值类的二(三)叉树定价模型则将每个时间点的价格变动分为2(3)个方向,由树的末端倒推计算出期权价格。当然,理论推导和数值模拟均已证明,当二叉树的时间间隔无穷小时,二叉树定价与BS定价是等价的。
对于美式期权,因为提前行权的特性,其定价公式本质上是一个动态规划的过程,这使得其定价的复杂度远大于欧式期权。美式期权上不存在封闭的解析解,通常借助数值计算方式,通过求一个可行的近似解逼近解析解来进行定价。例如,有限差分法通过差商代替微商,对方程以及定界问题离散化,把微分方程用一组差分方程来代替,最终通过迭代法求解差分方程。而美式二叉树,比如Cox-Ross-Rubinstein(CRR)模型,在计算期权价值时额外考虑是否提前行权。在每个节点上,需要比较提前行权的价值和继续持有期权的价值,取较大者作为该节点的期权定价。此外,对于一些结构较为复杂的期权,蒙特卡洛模拟也能很好地对其进行定价,该方法通过不断且多次模拟标的价格的变化路径以求得对应期权的价格。
不同美式期权定价方法在定价精度上区别较小,但在计算效率上却有较大差异。有限差分法需要求解一组差分方程,因此需要的计算时间较长。同时,蒙特卡洛方法也需要大量的模拟次数来尽可能地模仿现实市场中标的资产的价格波动。相较之下,CRR模型通过数值模拟的方法,避免了复杂的方程求解,计算上相对高效。1987年Barone-Adesi-Whaley(BAW)模型对BS模型进行扩展,将美式期权的价值分解成两部分。一部分是欧式期权定价,即通过 BS 模型进行定价;另一部分是由于美式期权可以提前行权而需要增付的期权金,通过变量替换将偏微分方程简化为常微分方程,实现了近似解析解,计算效率较高,在实际市场中被广泛应用于美式期权定价。
海外国债期权合约设计上多采用美式履约,从目前了解到的信息来看,中金所公布的国债期货期权合约草稿在设计上也遵循国际惯例。因此,本文实证部分模型使用上也基于美式结构。
(三)不同波动率估计方法
在期权的定价模型中,波动率是一个关键的输入参数,它描述了标的资产价格在单位时间内的变动性或不确定性。在BS模型中,期权价格与波动率的平方根成正比,估计波动率在期权定价、期权交易及风险管理中扮演着至关重要的角色。高波动率意味着更高的不确定性和潜在风险,而了解和管理波动率是期权交易成功的关键因素之一。
波动率可以由历史波动率来估计,也可以用隐含波动率来估计。历史波动率是基于过去一段时间内资产价格的实际波动情况来计算得到的,而隐含波动率则是根据期权市场价格反推出的波动率,是实际交易出的结果。
估算历史波动率,最简单的要数基于标准差的方式,其借助移动窗口,对每个窗口内资产收益率计算标准差,以此来估计波动率随时间的变化情况。但这种预测方法存在一个明显的问题,即资产价格的大幅变动会在波动率估计量的序列中保留一段时间后突然消失。
指数加权移动平均(EWMA)模型用滞后一期(期)收益率平方与滞后一期方差的加权平均来预测当前期的波动率,一定程度上解决了波动率预测中价格跳空的影响。而作为计量经济学中用于估计时间序列波动率的经典模型,自回归条件异方差(ARCH)和广义自回归条件异方差(GARCH)模型也能够捕捉到波动率随时间变化的特点,从而解决上述提到的问题。
近年来,机器学习技术也被用于估计波动率,包括随机森林、神经网络、遗传算法等。每种方法都有其优势和局限性,选择哪种方法取决于数据的可用性、计算资源和特定应用的需求。在实际应用中,投资者和风险管理者需要结合多种方法来获得更稳健的波动率估计。
实证研究
(一)国债期货历史波动率
本文选用2015年3月20日至2024年8月5日共2283个交易日的10年期国债期货收益率样本数据,计算国债期货历史波动率。其中,图1为EWMA、GARCH(1,1)模型计算的历史波动率,图2为20天、40天、60天的标准差波动率。从结果上看,不同方法计算出的历史波动率的变化趋势是相同的。波动率的聚集效应、均值回归特性在国债期货上也较为明显。
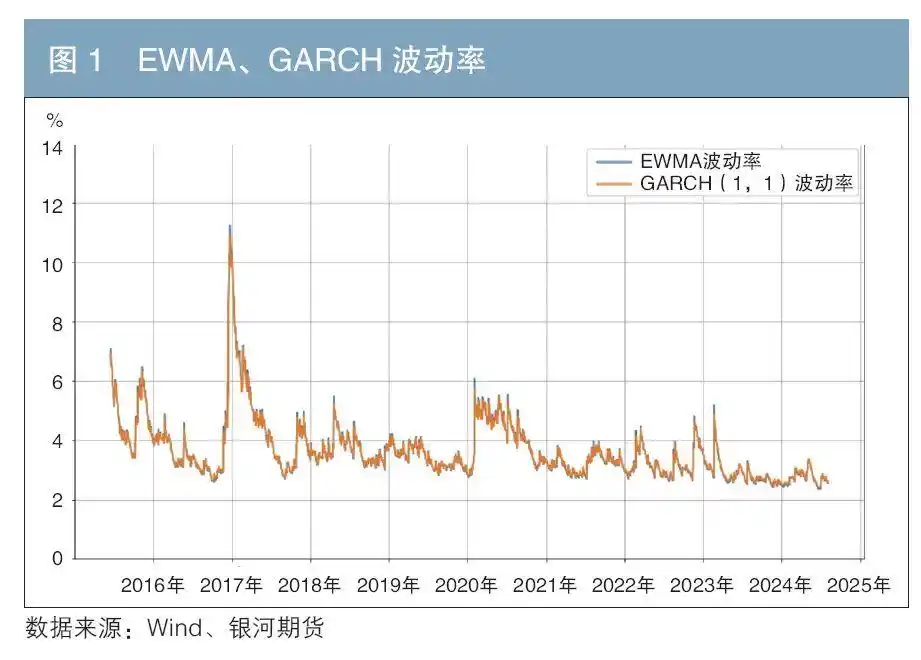
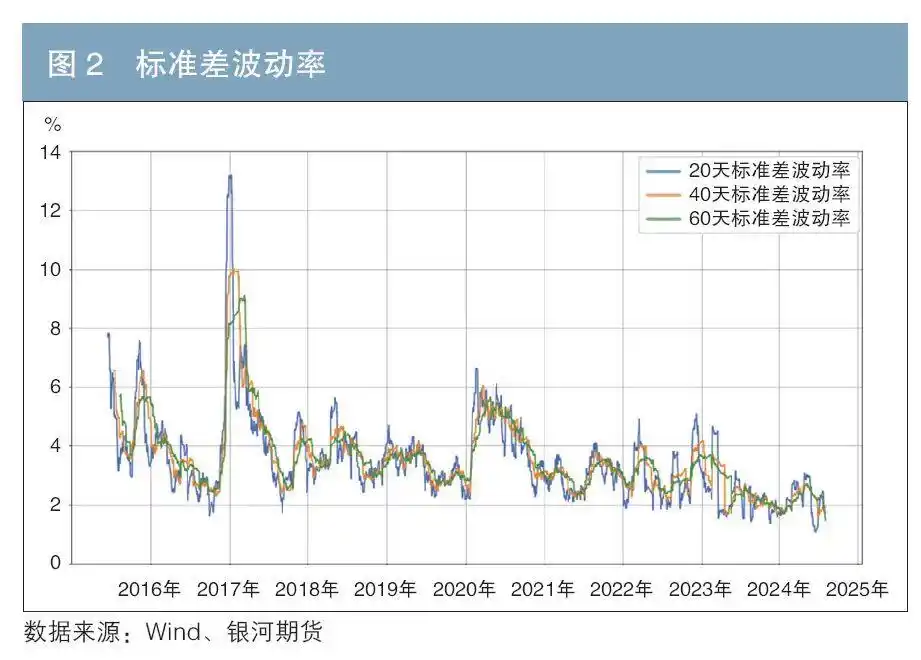
历史数据显示,波动率升幅最大的一次发生在2016年末到2017年初。彼时资金面收敛和央行流动性收紧预期引发投资者对债市去杠杆的担忧,叠加大宗商品价格上涨抬升通胀预期以及机构赎回增多等因素冲击,市场出现了恐慌情绪,引发了更多的止损盘和做空力量,市场波动率短时间内出现了快速攀升。
另一次波动率较大升幅发生在2020年初。新冠疫情暴发后,在货币政策超常规宽松的大背景下,10年期国债收益率一度快速下行至2.5%附近。随着股市走强、政府债券供给放量以及资金面逐步趋紧,国债收益率重新震荡上行,债市波动逐步有所下降。
(二)波动率估算方法的选择
前文提及历史波动率和隐含波动率在定义上的差异,且相较于历史波动率,隐含波动率与期权实际价格的关系更为直接。为了缩小期权理论定价与实际市场价格之间的差距,提升理论定价的精度,需要确认与隐含波动率最为接近的历史波动率计算方法。
在缺乏国债期货期权实际交易数据的情况下,本文通过对已上市且同为美式期权的铜期权合约模拟定价与真实价格走势的对比研究,发现GARCH和EWMA方法估计的历史波动率更接近隐含波动率(见图3)。而对于标的价格/期权价格波动频繁的合约(CU2409),GARCH比EWMA稍微好一些(见图3);但是对标的价格/期权价格比较稳定的合约(CU1912),EWMA明显优于GARCH(见图4)。
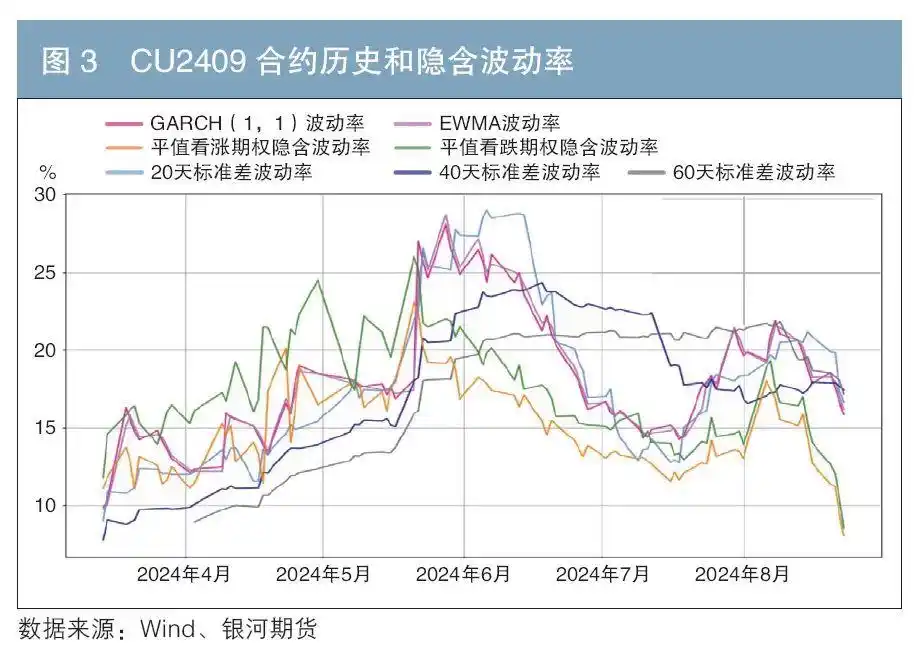
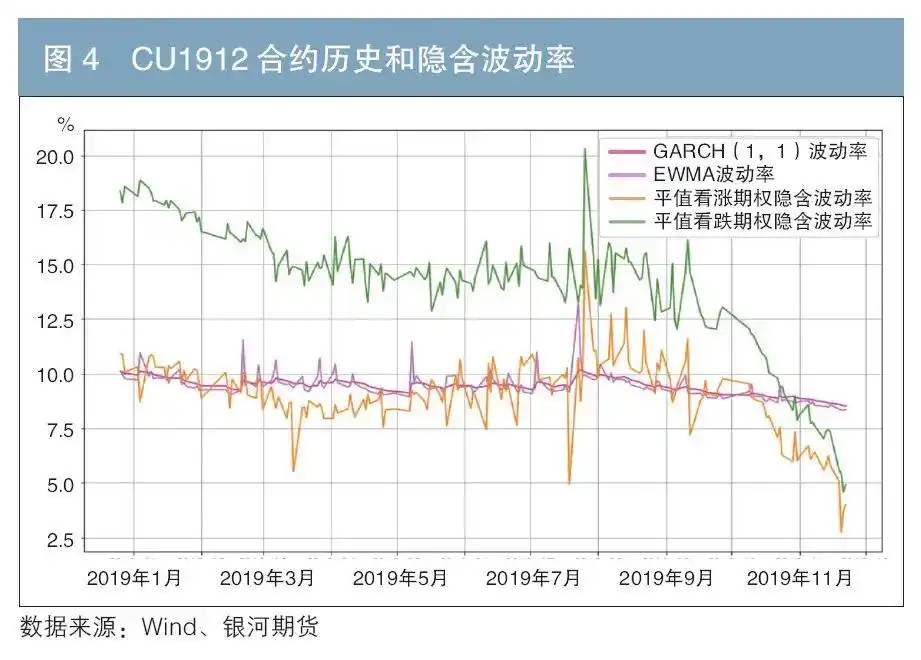
综合来看,笔者发现通过EWMA计算得到的历史波动率,在大多数市场环境中都是隐含波动率的一个较好的估计。因此,在对国债期货期权进行模拟定价时也采用EWMA方法来进行计算。
(三)国债期货期权理论定价结果与特征
经过上述讨论,我们选取被广泛应用于美式期权定价且计算效率高的BAW定价模型,其公式如下(以看涨为例):
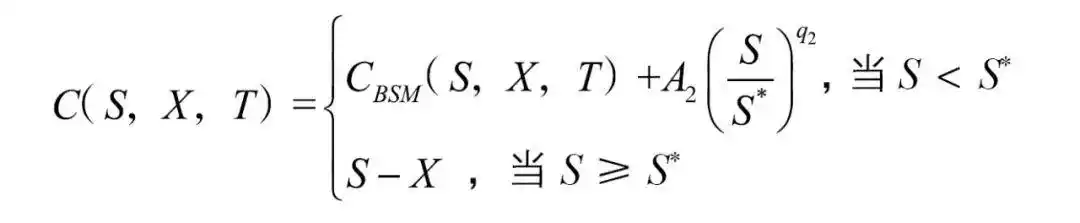
第一项是BS模型计算所得的看涨期权价格,第二项是提前行权需要增付的权利金部分。具体地,A2=S*/q2(1-e(b-r)TN(d1(S*))),其中
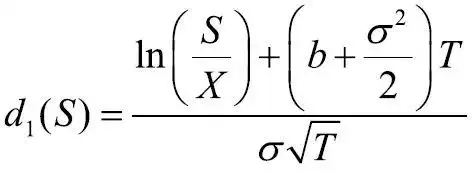
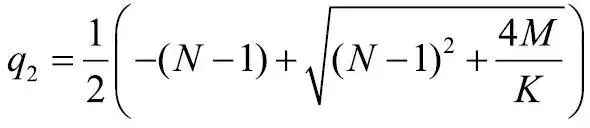
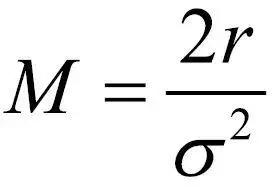
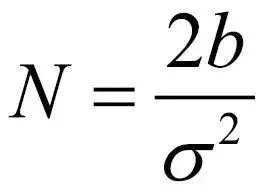
,K=1-e-rT。其中, S为标的当前价格, X为行权价,T为距离到期时间,b为持有成本,σ为定价所假设的波动率,r为无风险利率。S*为临界的标的资产价格,满足
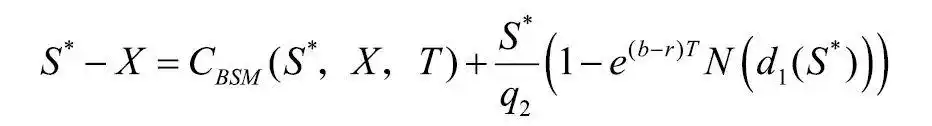
波动率估算方法选择EWMA模型。设收益率序列为rt,波动率序列为σt,则其公式为
其中,λ是衰减因子,取值范围在0到1之间。J.P. Morgan和Reuters通过最小化均方根误差(RMSE)推导出最优衰减因子,发现日数据集的最优衰减因子为0.94,月数据集的最优衰减因子为0.97。因此,本文采用 λ=0.94。
价格参数S采用10年期国债期货合约的价格,并通过四舍五入,选取与当天期货价格S距离最近的行权价格作为平值期权(ATM)。实值期权(ITM1、ITM2)和虚值期权(OTM1、OTM2)则根据中金所已公布的合约设计草稿分别在ATM基础上加减0.25、0.5。T为期权合约距离到期日的时间,选取上海银行间同业拆借利率(Shibor)作为市场无风险利率r,并从中查找距离T最近的期限利率,代入计算。
图 5 展示了10年期国债期货期权当月合约模拟定价的结果(以看涨期权为例)。可以看到实值期权由于其内在价值较大,所以价格始终高于平值和虚值期权。期权当月合约在刚完成换月后,由于其距离到期日的时间最长,时间价值最高,此时的期权价格往往也是阶段性的高点。但随着到期日的临近,时间价值逐渐衰减,期权价格也随之走低,直至到期日平值和虚值期权价格降至0。这一特征随着每次换仓呈周期性重复,也就是说,对于期权买方而言,代表时间价值的Theta值为负。
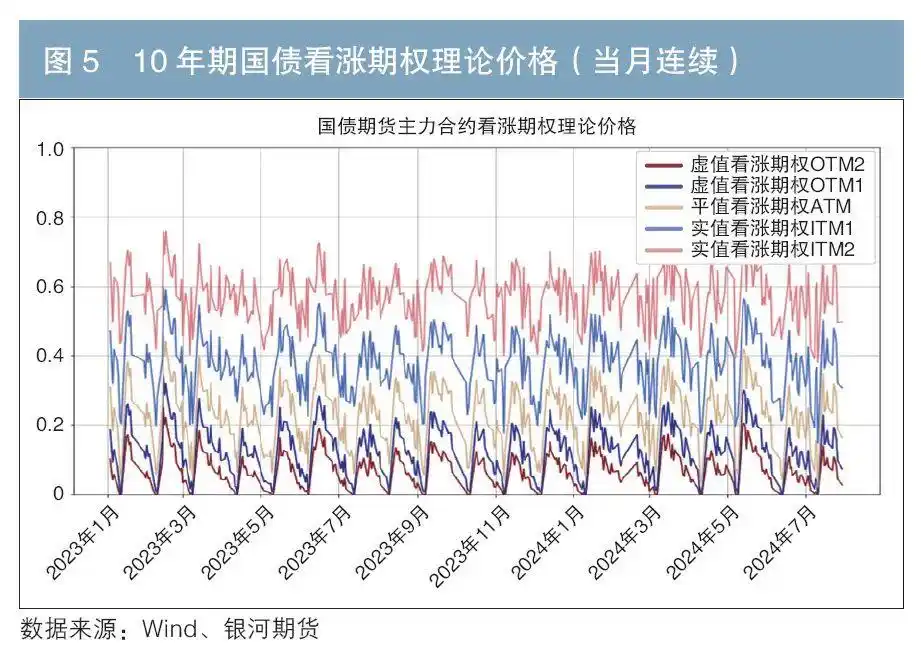
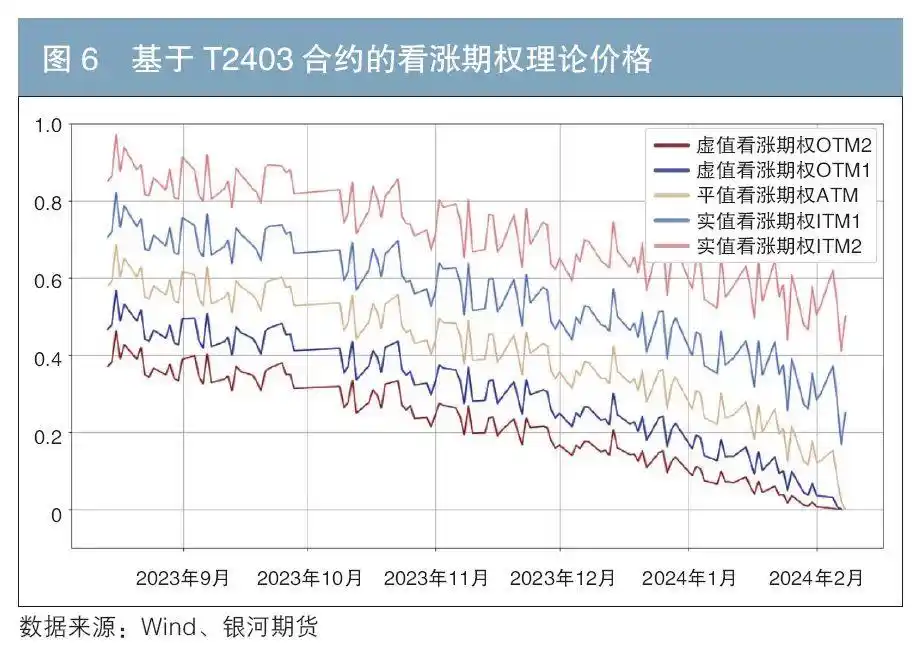
具体到单个合约,我们以10年期国债期货合约T2403为标的,按中金所合约设计规则,对应模拟期权的存续时间为在2023年8月第二个星期五的后一个交易日(2023年8月14日)至2024年2月第二个星期五(2024年2月9日)。从图6中我们可以更明显地发现期权价格随着到期日的临近,时间价值逐步衰减带动期权价格呈现震荡回落的趋势。且在合约快要到期时,平值和浅实值期权的时间价值衰减速度将有所加快,即Theta的绝对值会上升,对应价格下行斜率趋陡,时间价值衰减呈现非线性的特征。
我们还将期权执行价格固定在某一特定值,以此观察特定执行价下,期权与标的期货价格之间的联动性特征。以2023年8月14日为观察起始点,此时T2403合约价格为102.45。我们将执行价格分别固定为K1=102.25、K2=101.50(见图7、图8),发现随着T2403价格前期先跌后涨,看涨期权合约价格也随之有相同趋势的变动,即正Delta特征,而看跌期权价格则呈现反向变动,即Delta为负。
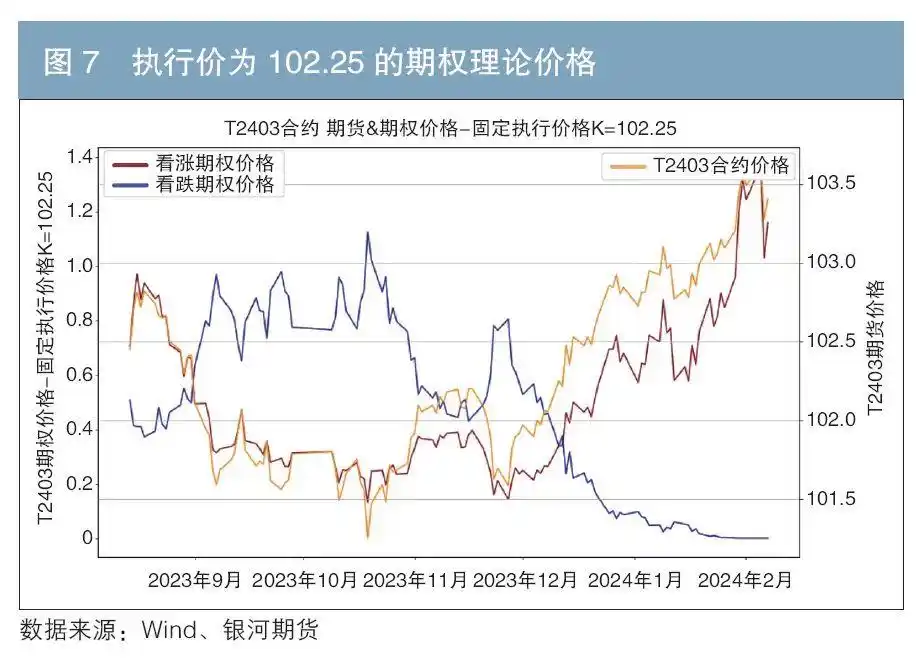
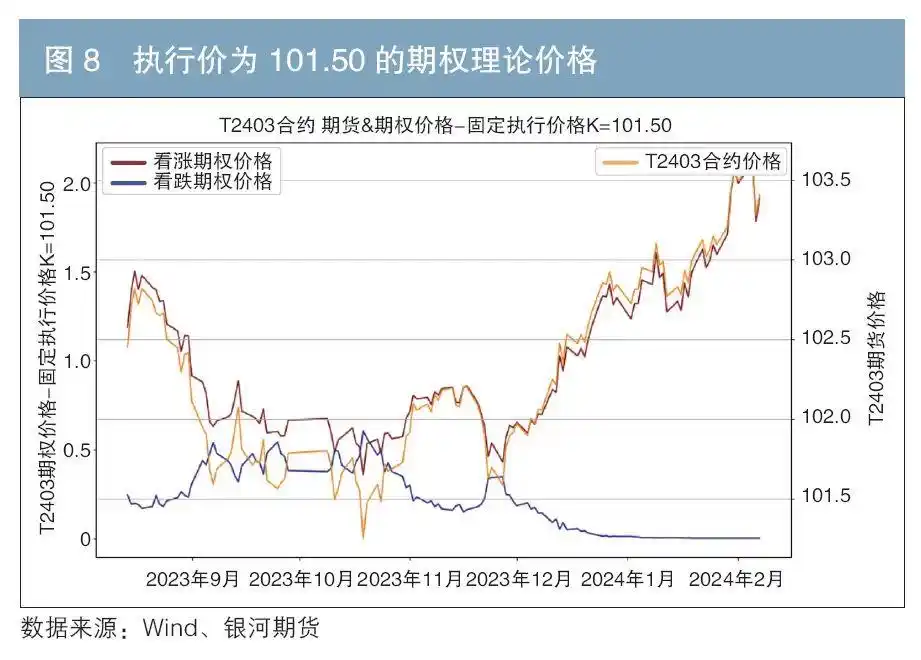
无论是看涨还是看跌,虚值期权Delta绝对值都较低,其价格对标的价格变化的敏感度也相对较低。比如2023年9月后,执行价格为102.25的看跌期权一度变为实值,其价格振幅明显大于同一标的但执行价格为101.5的看跌期权。
此外,从2023年12月开始,期货价格开始稳步上涨,对应两个看涨期权重新变为实值,价格联动性随着实值程度的加深和合约到期日的临近逐步上升,即期权Delta收敛于1;同时,看跌期权进入虚值状态,随着到期日临近,价格逐步趋于0,Delta也收敛于0。
总结
本文聚焦国债期货期权的理论定价问题,选用EWMA方法计算历史波动率并代入BAW期权定价模型,以中金所10年期国债期货T2403合约作为标的进行模拟定价。结果显示,本文估算的期权理论价格能够较准确地跟随期货标的进行有效波动。且不同行权价、不同方向下,时间价值衰减、期权价格与标的资产价格之间非线性联动的特征也较为明显。这为国债期货期权理论定价提供了一种有效的方法和参考。
市场实践中,国债期货期权的实际市场价格最终由供求关系决定,并受市场情绪等因素的影响。实际价格会随着市场条件的变化而变化,可能与理论价格存在一定偏离,这需要投资者在做风险管理和投资决策时格外留意。
近年来,随着我国宏观经济运行环境发生深刻变化,政府债券发行规模持续增加。但目前我国场内国债期权依然处于空白,现有对冲工具所能发挥的作用也存在一定局限性,无法满足投资者更多元、更精细的风险管理和投资需求。因此,有必要加快推动国内国债期权合约上市的进程,进一步健全债券市场的风险管理体系,让金融衍生品工具更好服务实体经济。
